Traditional methods for theorem proving using proof assistants like Lean have faced significant obstacles, such as private code, inaccessible data, and extensive computational requirements. These barriers have hindered research on machine learning techniques for theorem proving.
A groundbreaking paper has just removed these barriers by unveiling LeanDojo—an open-source Lean playground packed with toolkits, data, models, and benchmarks! 🚀
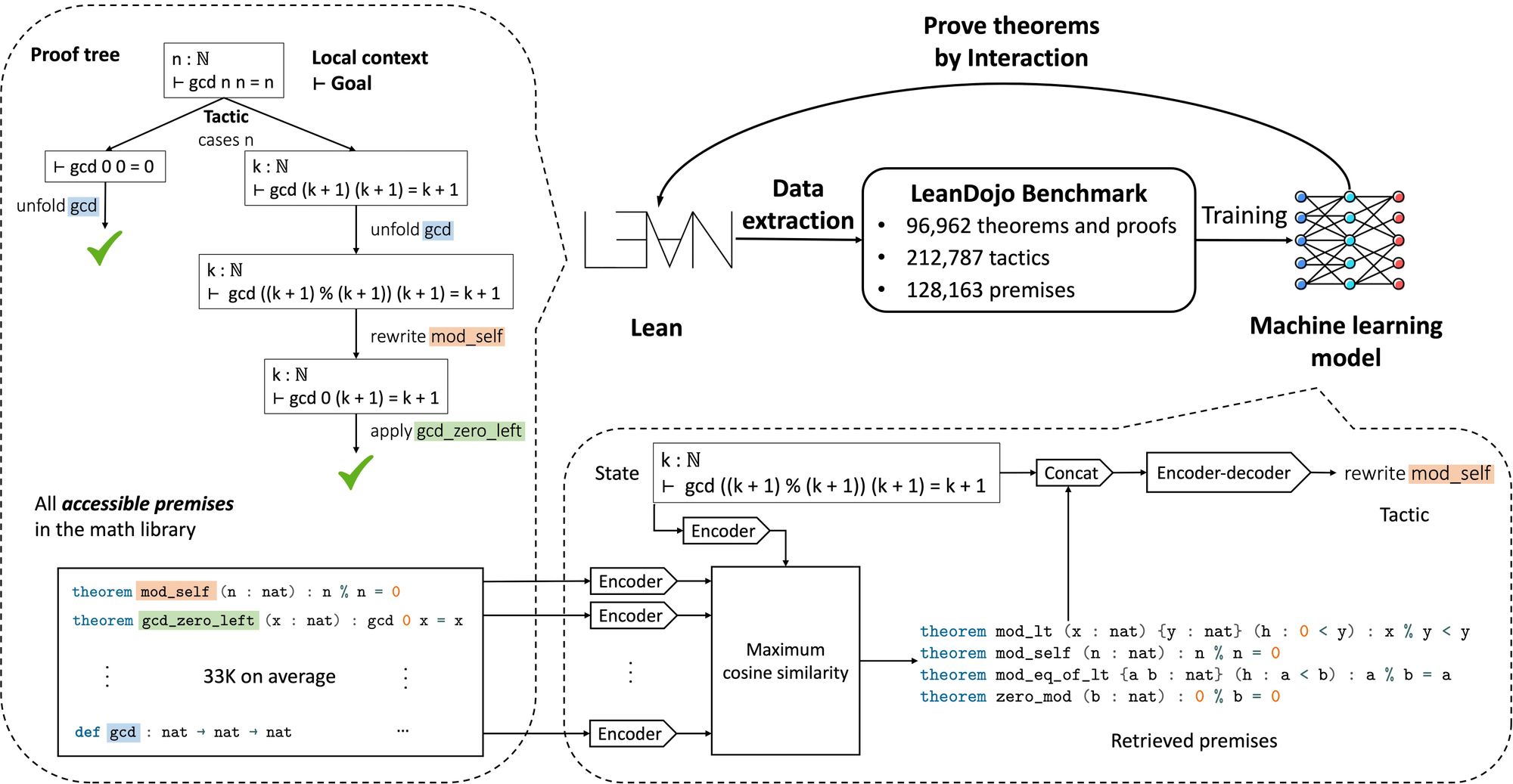
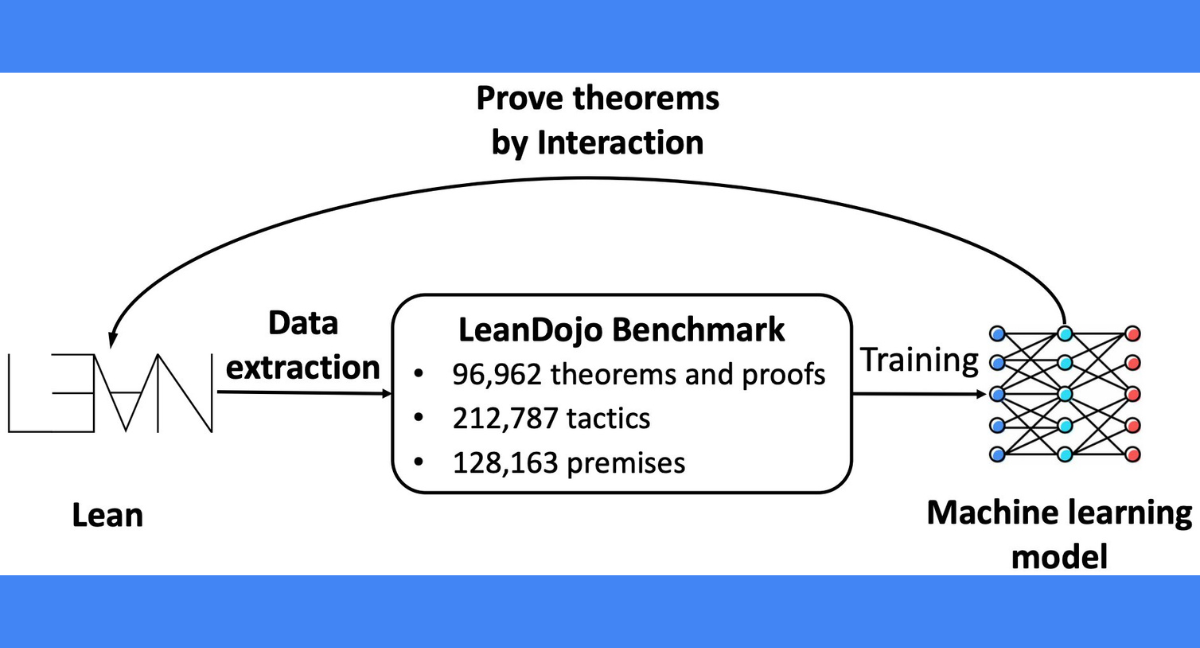
Top right: LeanDojo extracts proofs in Lean into datasets for training machine learning models. It also enables the trained model to prove theorems by interacting with Lean's proof environment.
Top left: The proof tree of a Lean theorem ∀�∈�, gcd n n = n, where gcd is the greatest common divisor. When proving the theorem, we start from the original theorem as the initial state (the root) and repeatedly apply tactics (the edges) to decompose states into simpler sub-states, until all states are solved (the leaf nodes). Tactics may rely on premises such as mod_self and gcd_zero_left defined in a large math library. E.g., mod_self is an existing theorem ∀�∈�, n % n = 0 used in the proof to simplify the goal.
Bottom: ReProver model. Given a state, it retrieves premises from the math library, which are concatenated with the state and fed into an encoder-decoder Transformer to generate the next tactic.
So, what makes LeanDojo so remarkable? Let's delve into its key features:
🎯Premise Information: LeanDojo Benchmark provides meticulously annotated premises—revealing where they are utilized in proofs and where they are defined in the library. This invaluable data addresses a major bottleneck in theorem proving: premise selection. Now, researchers can benefit from enhanced premise selection to boost their theorem-proving endeavors! 💡
🔀Challenging Data Split: To ensure an accurate evaluation, LeanDojo introduces a novel approach to data splitting. Randomly dividing theorems into training and testing sets can lead to inflated performance metrics, as LLMs might rely on memorizing similar proofs. LeanDojo's challenging data split necessitates models to generalize to theorems reliant on entirely new premises not encountered during training—a game-changer in advancing theorem-proving techniques!📈
LeanDojo transforms Lean into an immersive gym-like environment. It empowers provers to observe proof states, execute tactics to modify those states, and receive real-time feedback on errors or proof completion. This environment proves indispensable for evaluating, deploying, and even training provers through Reinforcement Learning (RL). The possibilities are endless! 🏋️♂️🔍🤖
ReProver: the world's first LLM-based prover enhanced with retrieval capabilities! Leveraging LeanDojo's program analysis, ReProver intelligently selects premises from an extensive math library. Remarkably, this groundbreaking prover requires only one GPU week of training, making it cost-effective and accessible to researchers. Say goodbye to proprietary datasets and welcome a new era of open-source LLM-based theorem proving! 🎉🔬
To validate ReProver's prowess, a new benchmark consisting of 96,962 theorems and proofs extracted from Lean's math library was constructed. This benchmark features a challenging data split, compelling the prover to generalize to theorems relying on novel premises never encountered during training. Experimental results unequivocally demonstrate the effectiveness of ReProver compared to non-retrieval baselines and even GPT-4. The future looks bright for LLM-based theorem proving!🔍✨
ReProver's impact extends beyond proving theorems. It has already made significant contributions to the formalization of theorem statements, assisting ProofNet in uncovering multiple bugs. Additionally, a groundbreaking LeanDojo ChatGPT plugin has been developed. This plugin enables ChatGPT to interact with Lean, facilitating the proof of theorems by interleaving informal mathematics with formal proof steps. While ChatGPT provides a more intuitive and human-like interaction with proof assistants, it still faces challenges in searching and planning for correct proofs. The possibilities for collaboration between humans and machines are immense! 🤝🤖💬
Exciting times lie ahead as LeanDojo revolutionizes the world of theorem proving! Researchers and enthusiasts alike can now access an open-source platform, explore the power of LLMs, and push the boundaries of mathematical discovery and formalization. LeanDojo's MIT license ensures that the advancements made with this platform can be freely used and built upon, fostering a collaborative and innovative environment for further research.
But LeanDojo's impact goes beyond its own ecosystem. Extracting data from any GitHub repository in Lean, including both Lean 3 and Lean 4, opens up possibilities for cross-referencing and analysis across various mathematical libraries and formalizations. Researchers can leverage LeanDojo's rich data, encompassing file dependencies, abstract syntax trees (ASTs), proof states, tactics, and premises, to gain deeper insights into the foundations of mathematics and uncover new connections.
The release of the LeanDojo Benchmark, featuring an impressive collection of 96,962 theorems/proofs, 212,787 tactics, and 128,163 premises extracted from Math lib, sets a new standard for evaluating and comparing theorem provers. Its challenging data split ensures that performance metrics accurately reflect a prover's ability to generalize and tackle novel problem domains. This rigorous evaluation fosters the development of robust and reliable theorem-proving systems.
Moreover, ReProver's remarkable achievements in discovering new proofs and identifying formalization bugs demonstrate the immense potential of LLM-based approaches. By combining the power of large-scale language models with intelligent retrieval mechanisms, ReProver is paving the way for automated theorem-proving systems that can augment human efforts in formalizing mathematics and uncovering hidden knowledge.
LeanDojo has also recognized the need for human-computer collaboration in theorem proving. The LeanDojo ChatGPT plugin enables ChatGPT to interact with Lean, bridging the gap between informal and formal mathematics. While specialized LLMs like ReProver excel in specific tasks, ChatGPT's flexibility and explainability make it a valuable tool for explaining error messages, receiving feedback, and exploring mathematical concepts in a conversational manner. This fusion of human intuition and machine assistance opens up new avenues for theorem proving and mathematical exploration.
The introduction of LeanDojo, ReProver, and the LeanDojo Benchmark marks a significant leap forward in the field of theorem proving. By removing barriers, providing open-source resources, and fostering collaboration, LeanDojo empowers researchers and enthusiasts to advance the frontiers of mathematical knowledge. The era of LLM-based theorem provers has arrived, and the possibilities for formalizing, exploring, and unlocking the mysteries of mathematics are boundless. Let's embark on this exciting journey together! 🚀🔍🌌
Read More:
LeanDojo: Theorem Proving with Retrieval-Augmented Language Models
We research, curate and publish daily updates from the field of AI. Paid subscription gives you access to paid articles, a platform to build your own generative AI tools, invitations to closed events, and open-source tools.
Consider becoming a paying subscriber to get the latest!